
以下文章摘抄至《基于短周期密集地震台阵观测的空间自相关法及其在粤港澳大湾区的应用》潘啟安 沈旭章
doi:10.11939/jass.20220003.
基于空间自相关法从粤港澳大湾区短周期密集台阵的21个观测点记录的微动信号中提取了瑞雷波频散曲线,并反演得到了广州市番禺区内布设的台阵下方1km深度范围内的浅层S波速度结构。结果显示:台阵下方0.25km深度以内的速度明显偏低,介于1.17km/s到1.59km/s之间;0.25-1km深度之间的速度平稳增加至2.88km/s,表明通过空间自相关法可以有效地获取观测台阵下方稳定可靠的浅层速度结构。因此短周期密集台阵技术与空间自相关法结合是在人口稠密的城市群地区进行地下浅层的精细结构探测的一种有效、经济、环保的手段,将在未来城市地区的浅层结构探测中发挥重要作用。
近年来随着我国城市化进程的全面推进,城市人口日益密集,超高型建筑、大型生命线工程在城市及周围林立密布,对基础建设的要求也越来越高,与此同时城市特别是超大城市的安全也已成为人们首要关注的重要问题。粤港澳大湾区作为广东省九市和香港澳门两个特别行政区组成的世界级超大型城市群,是媲美于东京湾区、纽约大都会湾区和三藩市湾区的全球第四大湾区,具有非常重要的战略地位。人口密集、经济发达、财富高度集中等特点都使得大湾区对地震地质灾害具有非常高的环境敏感性,因此探明大湾区城市的地下浅层结构,对于城市工程建设、灾害防治、地下空间的利用开发都具有极其重要的意义。
传统的浅层结构探测主要依赖于浅地表的各种主动源地震勘探方法以及钻孔取样和测井等技术,诸如浅层反射、浅层折射以及主动源面波勘探等这些主动源勘探方法的优势是空间分辨率高,但人工和时间成本较为高昂,探测深度一般无法达到千米尺度而且相当一部分主动源勘探方法不宜在人口密集的城市内开展,导致这些方法在城市区域的应用明显受限。短周期密集台阵探测技术的迅速发展为探测粤港澳大湾区这种超大城市群的高精度地壳结构提供了一种可靠的技术路线。相较于宽频带流动台阵,短周期密集台阵的台间距仅为数十米至数百米,观测时间也仅为数天到数十天,且单台仪器价格便宜,可以一次性投入大量的仪器设备进行浅部精细结构探测,因此在人口密集的城市地区具有非常明显的优势和广阔的应用前景。同时微动勘探方法的广泛应用也为密集台阵数据的处理提供了理论依据。
地球表面由于受到人类活动或者自然扰动无时无刻都在发生微小的振动,简称微动,其振动幅度通常只有几微米,因此很难被人体所察觉。微动的震源根据产生原理分为两种,即自然因素和人为因素所产生的发生源:前者如风吹、雨打、海浪和火山活动等自然现象所产生的低频(<1Hz)微动信号,通常称为地球脉动;后者如人的行走、车辆行驶、工厂加工、交通运输以及建筑施工等人类活动所产生的高频(>1Hz)微动信号,一般称为常时微动。微动在地下介质传播的过程中必然携带着传播途中介质性质的信息,因此通过对微动信号的处理和分析能够获得近地表速度结构。相比传统的地震勘探方法,微动探测更为方便,同时还避免了浅部高速层的屏蔽作用,是城市浅层结构探测的理想方法。而且微动勘探方法中常用的空间自相关(spatial autocorrelation,缩写为 SPAC)法在浅层结构探测中已经取得了良好的应用效果(孙勇军等, 2009)。例如,徐佩芬等(2009,2012)利用SPAC方法探查煤矿工作区的陷落柱、深圳市地铁的“ 孤石 ”以及地层分层和隐伏断裂构造,取得了非常好的应用成果。
短周期密集台阵技术近些年来在国内外不同区域都开展了大量观测并取得了一系列重 要研究成果。例如:美国加利福尼亚州南部洛杉矶地区长滩市的长滩( Long Beach)密集台阵,在7km×10km范围内布设了5300个单体式短周期地震仪组成的超密集台网,基于其观测资料,已经开展了石油储层探测、地壳精细结构以及地震孕育环境等多方面的研究(Lin et al,2013),这是迄今为止国际上最成功的短周期密集台阵;由南加州大学在南加州地区布设的包含1108个垂直检波器的密集台阵,已经开展了断裂带精细结构探测研究,Roux 等(2016)利用该地区2-4Hz的群速度所获反演结果揭示了圣哈辛托(San Jacinto)断层及其周围结构性质的纵向和横向变化;“地学长江计划”在长江安徽段布设了数百台短周期地震仪观测多条剖面,进行浅部结构成像和壳幔结构的研究(Wei et al,2018);Li等(2016)在五大连池布设了由43台便携式三分量短周期地震仪组成的密集流动台阵,并利用背景噪声层析成像获取了五大连池地区的上地壳高分辨率三维精细波速结构;Li等(2018)利用在唐山历史震区布设的短周期密集台阵采集的数据研究唐山大地震,其结果提供了唐山震区的高分辨率速度结构、微震事件位置和震源机制解,对揭示唐山地震动力学的潜在影响因素具有重要的意义。这些短周期密集台阵的项目均取得了较好的探测成果,表明密集台阵技术能够有效地提高浅层结构探测成像的分辨率(雷华等,2019)。
空间自相关(SPAC)法最早是由日本著名地震学家Aki(1957)提出的基于平稳随机理论进行微动探测的一种重要方法,随后基于SPAC方法衍生出多种数据处理方法,例如:Okada和Suto(2003)详细介绍了可以采用不规则台阵进行探测的扩展的空间自相关法(extended SPAC,缩写为 ESPAC),该方法无需满足圆形台阵的布设条件,可以将台阵布设成线性、L型或者任意不规则形状,野外适用性更强;Asten(2006)提出了不需要提取频散曲线而直接通过SPAC系数拟合进行剪切波速度结构反演的多模式空间自相关法(multi-mode SPAC,缩写为MMSPAC);Asten等(2019)还提出了一种将一组频率相干谱转换为波数相干(wavenumber-coherency,表示为kr)谱,该方法可以对来自多对传感器的谱进行空间平均,而不考虑对谱的空间分离差异,通过直接拟合实测与模型的波数相干谱并进行迭代来确定最优的层状地球S波速度模型,该方法也被称为krSPAC方法。同时,随着计算SPAC系数的方法不断地发展,Okada(2006)也对SPAC方法台阵布设所需台站数量问题进行了探讨和研究,结果表明相对于多个台站的台阵来说,三个台站的圆形台阵是最有效的。
考虑到SPAC方法经济环保、原理简单、操作便捷等优势,而且在密集台阵中采用SPAC方法进行上千米尺度的速度结构成像研究较少,本文尝试将该方法应用于粤港澳大湾区短周期密集台阵的微动资料处理,进行台阵下方的浅层速度结构成像,以验证该方法在密集台阵中应用的有效性和实用性,并为台阵区域提供可靠的S波速度结构。
Aki(1957)提出空间自相关(SPAC)法时认为,复杂的微动是一种平稳随机过程,是一种随时间t和位置ξ(x,y)而变化的自然现象。若某时段所记录的微动数据可看成平稳随机过程的样本函数,则微动的谱可以看成具有各种角频率ω和波数k的相互独立的波的连续和:
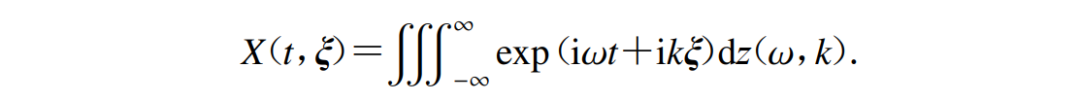
式中。ω为角频率,k为波数,z为正交随机过程。从上式可以看出,角频率 ω和波数k作为函数彼此相关,随机过程z仅在曲线[ω , k(ω)]上有意义。微动中的主要成分是面波,且其中一种面波模式(通常是基阶面波)占主导地位。
设在A和B两个不同的点观测到微动,两个点的位置矢量分别为η和η+ξ ,ξ 为两点间的位置矢量,A点的微动记录X(t,η)和B点的微动记录X(t,η+ξ)可以根据式(1)给出,则A与B两点间的空间自相关函数则可定义为:

其中
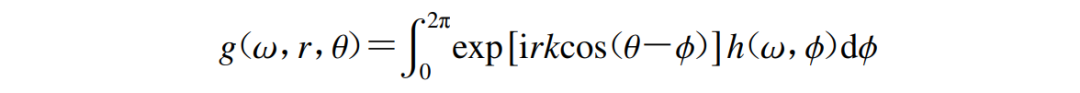
被称为空间协方差函数,该函数可用于计算角频率为ω的A和B两测点的微动协方差。从数学上看,式(3)意味 着 g(ω , r,θ)的值取决于微动能量场内可能变化的频率 -方向谱密 度 h(ω , φ)。这就有必要检查指定时段内观测到的数据是否满足时间上平稳的假设。为便于进行这种检查,在对数据进行详细分析之前,应先将观察到的所有数据块划分为多个短时段的 功率谱使用直接段或块平均方法(Capon,1969)进行估算。
定义O点为坐标原点,以O点为中心在半径为r的圆周上布设若干个测点,组成一个圆 形台阵。基于圆周上所有测点观测到的微动计算S(r,θ)而后取平均,即:
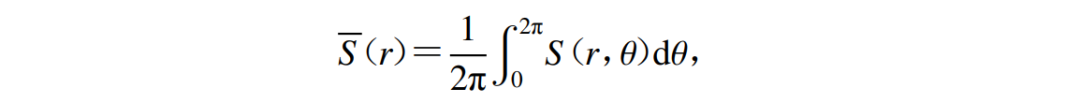
空间自相关系数ρ(r,ω0)定义为

式中:r为台间距,ω0 为角频率,c(ω0)为相速度,J0为第一类零阶贝塞尔函数。从这个空间 自相关系数的计算公式可以看出,空间自相关系数与相速度之间的关系是通过第一类零阶 贝塞尔函数确定的,因此,基于各种经过窄带滤波器处理的微动记录求出空间自相关系数 ρ(r,ω0),即可计算出与这些中心频率相对应的相速度c(ω)。这就是利用空间自相关法提取频散曲线的理论依据。
经过近些年的发展,基于空间自相关法也发展出在频率域中空间自相关系数的计算方法,计算公式为

式中,S(r,θ,ω)为圆心测点记录的微动数据与圆周测点记录的微动数据的互功率谱,S0(0,ω)为圆心测点记录的微动数据的自功率谱,Sr(r,ω)为圆周测点记录的微动数据的自功率谱。频率域计算出来的空间自相关系数与时域计算出来的一样,从结果来看二者是等效的。频率域计算空间自相关系数的方法,相对于时间域计算空间自相关系数的方法来说,其最大的优点在于未进行窄频带通滤波,对微动数据进行一次傅里叶变换之后就完全在频率域内进行计算,很大程度上提高了空间自相关系数的运算效率。
2021年初广东省地震局牵头在粤港澳大湾区进行大规模浅层三维结构探测,在广州、佛山、东莞三市的部分城区成功布设了长60km,宽60km,总面积为3600平方千米的大型短周期密集台阵。本次观测中所布设的短周期密集台阵的台站数量大,布设周期较长,因此分三批陆续在北京时间2020年12月至2021年2月期间进行滚动观测,虽然每一批仪器的 观测时间并不一致,但每个台站的观测数据 均保证在三天以上,且相邻两个台站的间距 均为0.75km左右。
为了测试SPAC方法应用于短周期密集台阵的效果,本文选取台阵中布设均匀、地形起伏较小的区域内地震仪所记录的微动来进行数据处理,并对该区域进行S波速度结构反演。在本研究中我们选取如图1左下角插图中的小黑框所圈范围内的观测点进行数据处理,台阵中的台站分布较规整,平均台间距为0.75km,包含21个短周期地震仪。这些台站采集了2021年1月4日至2021年1月 10日期间共7天的微动数据。为了充分利用所采集的数据,从中选取每日凌晨 2点至3点、3点至4点这两个受干扰较少时段的数据,并对7天的微动数据进行相同处理,最终获得这7天内每天2个共14个速度剖面进行平均,将其作为台阵下方的S波速度剖面。

图 1 研究区短周期地震台站(倒三角形)分布示意图
短周期密集台阵布设时采用中国深圳面元智能科技有限公司生产的 SmartSolo IGU- 16HR 3C三分量短周期地震仪和美国 Fairfield Geotechnologies 公司生产的 Zland 3C三分量便携节点地震仪,两种地震仪的主要指标列于表 1。
表 1研究区所用地震仪的主要性能指标

粤港澳大湾区位于珠江三角洲沉积区。珠江三角洲地处广东省中南部,是我国第二大三角洲,其中浅地表沉积的岩土类型多为覆盖于基岩之上的覆盖土,只有少部分基岩处于出露状态,同时大湾区埋深较浅的区域广泛发育淤泥、淤泥质岩及松散沙土,形成历史短,沉积物厚度较小,在珠江三角洲的亚热带季风气候导致的高地下水位下非常易于发生地质灾害。
选取位于广州市番禺区新城亚运体育综合馆附近的一块布设了21个短周期地震仪的区 域(22°55′48″N-22°57′00″N,113°24′00″E-113°27′00″E)作为研究区,该区内地形条件 和人为因素干扰较小,可被视为台间距为0.75km的规则的短周期密集台阵,满足空间自相关(SPAC)法的应用条件(Okada,2006)。Aki(1957)最初提出该方法时的理论要求是在圆形台阵的圆周上布设无数多个检波器,但这在实际的野外工作中确实难以实现。Okada(2006)在应用SAPC方法时对台阵的布设方法进行数值评估,其结果表明三台站圆形台阵是在观测点较少的情况下使用SPAC方法比较有效的台阵组合方式。由于野外工作条件所限,台阵实际布设时很难按照理想的情况进行,只能根据实际条件选取合适的台阵布局,有时甚至只能构成三点台阵,即圆周上只有两个测点,这种情形也曾取得较好的结果(王振东,1990)。本次布设的短周期密集台阵在应 用SPAC方法进行研究时无法按照国内最 常用的嵌套三角形台阵进行组合(任彦宗 等,2021),本文采用图2所示的台阵组合(类比嵌套三角形台阵,本文中称为嵌套正方形台阵)进行空间自相关系数的计算,最终得到五种不同半径的台间距组合所计算的空间自相关系数,对其进行平均 时可使所得结果更加平滑、可靠。

图2 空间自相关法台阵( a )及不同台间距(b−f)下的台站对组合示意图
图3a显示了本研究中所采集的部分原始微动记录。首先对单个台站的微动数据进行预处理,具体步骤包括重采样、去仪器响应、去毛刺、去均值、去线性趋势、波形尖灭、带通滤波并将微动数据的时间序列按照一定的长度裁剪成等长的片段进行时间均一化等。为了统一不同仪器的采样率并使数据量减小,按50 Hz对数据进行重采样,由于使用两种不同的地震仪,因此在重采样之后对数据进行去仪器响应、去毛刺、去均值、去线性趋势和波形尖灭,消除由于尖峰、非零均值、基线漂移、长周期线性趋势以及谱域假象所造成的 影响。对垂直分量的微动进行0.4-6Hz的带通滤波,将数据限制在此频率范围内,从而提 高信噪比。图3b为相应的微动数据经预处理之后的结果。最后将处理后的微动记录的垂直分量按照360s的时间长度进行分段,总共分成19段数据,每两段之间有180s的时间重叠,这样分段能使最终平均后得到的结果更加准确可靠。

图3 原始微动记录(a)和预处理后的微动记录(b)
将经预处理的微动数据进行两两组合即可计算空间自相关系数。首先,将九个台站数据 计算所得的36个空间自相关系数按照不同的台间距进行分组,可以分为五组;然后,将每组 的空间自相关系数分别进行方位平均,得到平均空间自相关系数,此即为一个台间距下的空间自相关系数;最后,分别计算预处理时截取的19段数据的空间自相关系数并进行平均得 到该台站对的最终的空间自相关系数。图 4 给出了实测的方位平均计算之后所得的空间自相关系数以及进行平滑(Savitzky,Golay,1964)之后的空间自相关系数。
从图4可以看出,由五种不同的台阵组合计算出来的空间自相关系数并非整条自相关系数都能与贝塞尔函数拟合很好,而且从空间自相关系数曲线判断与贝塞尔函数的拟合效果多依赖于人为判断,其中自相关系数曲线与贝塞尔函数相似的部分即为拟合较好的部分。但是空间自相关系数与贝塞尔函数的拟合比较复杂且困难,因此本文采取极值点计算法提取 频散曲线。

图4 五种台间距下的台站对的实测空间自相关系数 ρ(a)以及平滑后的空间自相关系数 ρ(b)
极值点计算法是Aki(1957)最初提出的频散曲线拟合方法,即找出标准的第一类零阶贝塞尔函数f 和每条空间自相关系数的极值点所对应的横坐标值x,然后每条自相关系数曲线对应一个台间距 r,这样代入公式x=2πfr/c(f)就能得到不同频率所对应的相速度,从而得到频散曲线。前人研究已经证明在 r 值离散性不大的情况下使用这种方法提取频散曲线可以得到约束较好的结果,并且利用这种方法提取频散曲线的稳定性很好(刘庆华等,2016)。在本文提取频散曲线的过程中,由于台间距的组合形式较多,由微动数据计算出来的频散曲线数量较多,且频散曲线的稳定性较好,此处仅展示其中一条,图 5 所示即为其中一个台阵组合的观测频散点以及其多项式拟合出来的频散曲线。

图5 根据空间自相关系数零极点计算得到的观测频散点及拟合频散曲线
瑞雷面波反演主要是通过面波的频散特性获得地下介质性质的过程。面波频散是介质层厚、密度、S波速度以及P波速度的函数(Xia et al,1999),而瑞雷面波频散对S波速度最为敏感,P波和密度的影响可忽略不计。另一方面, S波速度结构不仅对于研究地球内部的物理性质、地震波的传播和地球演化等方面具有重要的意义,同时也是工程勘探和抗震研究的重要参考模型。
本文采用基于最小二乘的线性迭代反演方法,通过PROGRAMS. 330软件包来实现(Herrmann,Ammon,2002)。整个模型是厚度为1km 的层状模型,初始模型参考该地区前人相关研究的地质资料、广东省地层结构并结合该地区的经验公式综合考虑后给出。假设地下 介质为泊松固体,密度结合前人研究设定为 2.7g/cm3(裴文,2011),首先设定所有层的S波速度均为1.955 km/s,P波速度按照公式Vp/Vs=1.73计算得到,经过一次线性反演所得到的 速度结构被作为初始模型再次进行反演。图6显示了反演所得到的其中一个台站下方的S波速度结构。
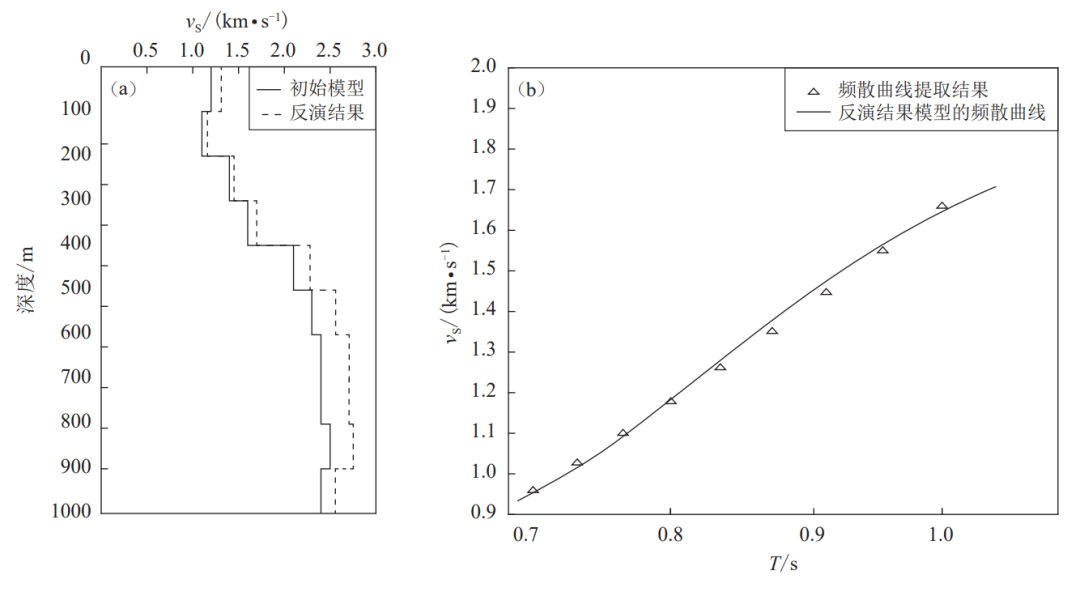
图6 初始模型和反演所得的S波速度结构(a)及观测频散点和反演的频散曲线(b)
将选取的所有台站数据进行处理,每个由九个台站组成的圆形台阵经过上述的数据处理后均能得到一个S波速度结构,因此对于时段相同的微动数据经处理后即可得到五个S波速度结构。将所得到的S波速度结构按照所选取台站的平均台间距0.75km进行排列,即可得到这条剖面线下方的速度结构,如图7所示。
在实际反演过程中,我们发现该频带内的频散曲线仅对0-1km深度范围敏感,因此在本次研究中反演该剖面1km以上的地下S波速度结构。图8为基于所选取台站在4日至10日这7天内每天2点至3点、3点至4点记录的数据所得到的14个速度结构的平均结果以及这14个结果的标准差。可以看出,该地区对于相同的台阵组合,每个不同时段的微动数据通过SPAC法提取频散曲线所反演的速度结构基本无太大变化,说明在该区域内应用SPAC法探测台阵下方介质的速度结构结果是稳定的。台阵下方的速度结构大致可以分成三层:第一层(0-0.25km),Vs在1.17km/s到1.59km/s之间,在0.1km深度处发育一个明显的低速层(Vs=1.18km/s);第二层(0.25-0.37km),Vs介于1.59-2.21km/s之间,且该速度层比较平整均匀,推测该层岩性较为均匀,波速随着深度平稳增加;第三层(0.37-1km),Vs处于2.21-2.88km/s之间,波速随着深度增加呈先增加后减少的趋势,中部(0.53-0.88km)发育一个高速层(Vs=2.88km/s)。
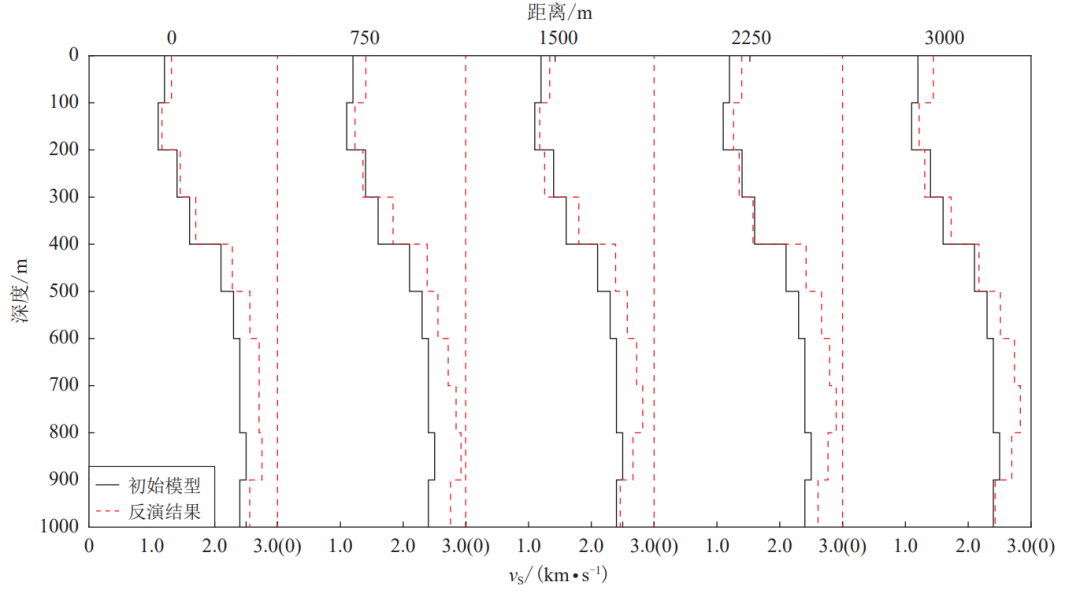
图7 按照台间距排列的S波速度结构(以第一个速度结构作为剖面线的起始点)
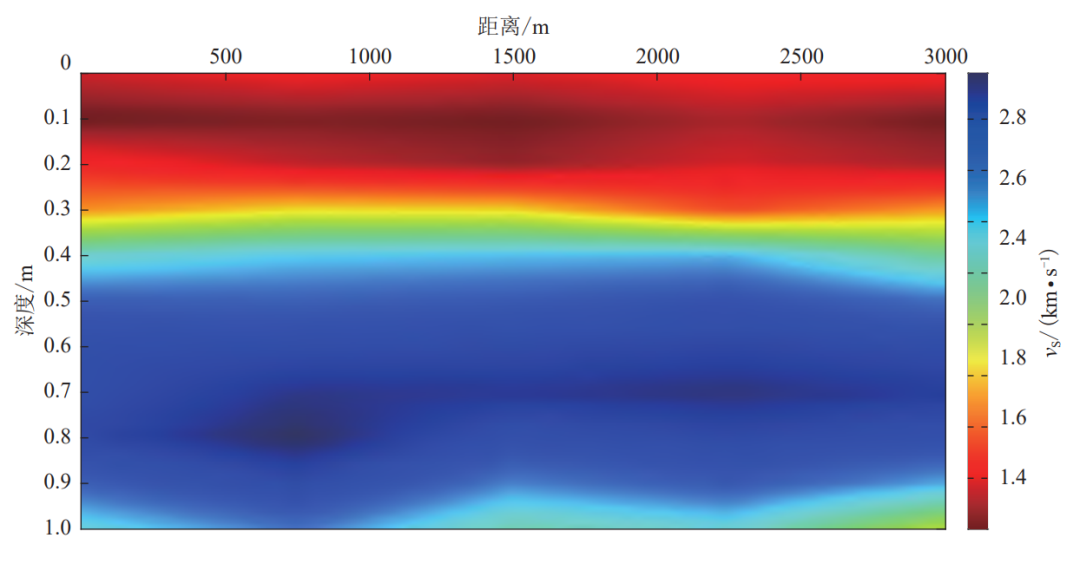
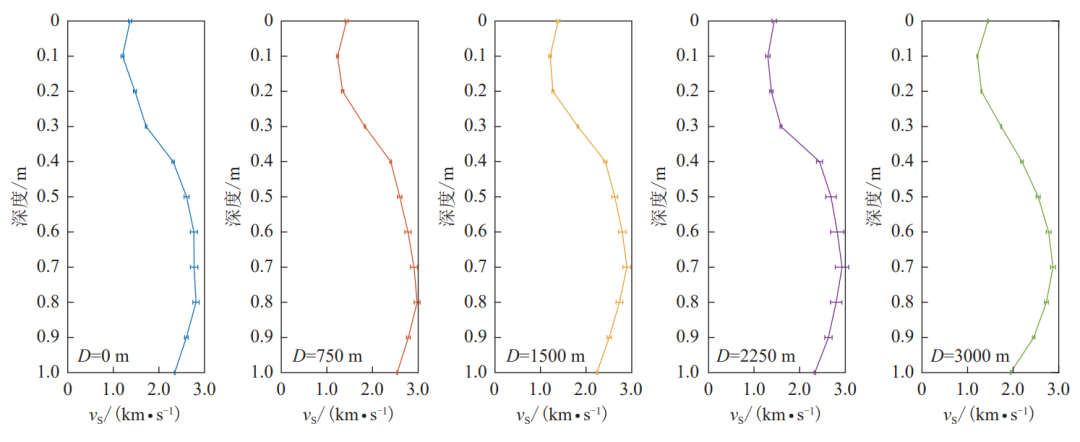
图8 S波速度结构(a)和标准差(b)(图中 D 为速度结构的距离)
从图8的S波速度结构中可以看出,本文方法所获得的S波速度结构基本反映了研究区的地质特征,可以与该地区以往的测井、钻孔以及其它地球物理方法的研究结果进行比较,但由于本研究仅使用了布设的短周期密集台阵非常小的一部分数据资料,用于计算方位平均的台站对数量并不多,导致了曲线拟合过程中数据点离散,影响了最终结果的精度,而且台间距也限制了瑞雷波的周期,可靠的探测深度范围估计在 0.1-0.9km,0.9km 以下的结构则难以探明。此外,台阵数据覆盖区域范围较小,结果无法反映整个大湾区的地质结构及 特征,在后续工作中我们将对粤港澳大湾区密集台阵的资料进行进一步的处理。
本文利用空间自相关法从布设在粤港澳大湾区的短周期密集台阵部分台站所记录的微 动数据中提取了瑞雷波频散曲线,在频散曲线的提取过程中基于实际观测点分布选择了合适的台站,以非传统的台站组合方式组成嵌套正方形台阵用于进行空间自相关法的应用研究,这是对空间自相关法在实际应用中的一种尝试,有望将空间自相关法与短周期密集台阵相结合应用于城市区域浅层结构探测中。通过对空间自相关法提取的频散曲线进行反演得到S波速度结构,并且结合几个台阵组合所得的S波速度结构得出台阵下方剖面的速度-深度图。
研究结果显示,空间自相关法与短周期密集台阵结合可以获取密集台阵下方比较可靠的S波速度结构,这表明通过空间自相关法可以在未来的城市群深部探测、地下空间开发利用、工程场地分析、灾害预防等方面开展更多研究,具有非常广阔的应用前景。同时空间自相关法相比于传统面波方法不需要人为的震源激发,可以有效地降低成本、减少噪声,是一种低碳环保、经济可靠的地球物理探测手段。
本研究仍然存在一些问题值得关注。短周期地震仪采集的微动数据可能与传统的宽频带地震仪有较大的区别,未来有必要在相同区域对两种仪器采集的微动数据分别使用空间 自相关法进行数据处理,将所得到的速度结构进行对比,以有效检验短周期地震仪的精度及结果的稳定性,因此如何科学地应用短周期地震仪采集的微动数据仍然是一个值得研究的复杂问题。同时,由于反演的多解性,最终所得结果可能与实际的结果有一定差异,因此需 要综合多种地球物理资料和地质资料进行分析解释。例如,采取不同的微动勘探方法对短周期密集台阵采集的微动数据进行成像,用背景噪声互相关成像及频率-波数法等将不同微动 勘探技术相结合甚至利用重力、磁法、电法等其它地球物理方法对大湾区进行联合勘探,探寻短周期密集台阵数据处理的最优方法。需要说明的是,本研究所处理的数据仅仅只是粤港澳大湾区密集台阵中的一小部分,旨在测试空间自相关法应用于短周期密集台阵进行浅层结构探测的可行性。从本文结果来看在密集台阵中空间自相关法所获结果比较稳定、可靠,未来将使用该方法对整个大湾区所有台站的资料进行处理分析,以得到大湾区更大范围的地下浅层精细结构。




