以下文章摘抄自《基于密集线性台阵的背景噪声成像在明光市城市活断层调查中的应用》
倪红玉, 郑海刚, 赵楠, 邓宝, 缪鹏，黄显良, 李俊伦
Doi：10 . 6038/cjg2022P0947 .
近年来，短周期密集台阵被动源探测技术逐渐成为地壳精细结构探测研究中的重要手段。为了探讨其应用于城市活断层调查在勘探尺度的有效性，在横跨安徽省明光市郯庐断裂带东界两条主干断裂位置，沿同期的主动源S波反射剖面，安徽省地震局和中国科学技术大学联合布设了一条由133个短周期地震仪组成的被动源密集测线。我们通过该被动源测线获得了约28天的连续波形记录，并采用一种新的线性台阵背景噪声成像方法——拓距相移法提取了10Hz~2.0s宽频的基阶Rayleigh波相速度频散曲线，利用得到的宽频带频散曲线，我们反演了近地表1.3km以浅的高分辨率S波速度结构，并与基本重合的主动源S波反射剖面以及地质资料等进行对比，验证了反演结果的可靠性，同时进一步分析了郯庐断裂带东界两条主干断裂的断层特征，结果表明：(1)被动源与主动源反演结果在近地表100m以浅高度一致，且被动源的反演深度更深；(2)池河—太湖断裂是隐伏于深部的走滑断裂和浅部伸展断裂的综合反映，浅部为倾向北西的正断层，向上穿透第四系地层，可能为活动断裂；(3)拓距相移法能有效拓宽频散曲线的提取频带，保证浅部结构具有高分辨率，同时大大加强对深部结构的约束，该方法能够获得可靠的地下结构反演结果，可以作为城市活断层调查的一种新的有效手段。
浅层地壳是与人类生存发展密切相关的区域，研究数百米以浅的S波速度结构对于场地分类、强地面震动模拟、地震危险性评价等抗震设防工作，以及矿产能源、地下空间安全等相关领域都具有重要意义（Flores-Estrelletal.，2007；Lietal.，2014；洪德全等，2017；王伟君等，2012；罗磊等，2019）。此外，在城市活断层调查项目中除了探测地表断裂和隐伏断裂深部形态的要求外，还需要提高地壳浅层目标异常体的探测精度，在研究深部结构时，也需要去除浅层结构的干扰，因此高分辨率的浅层速度结构还可以为城市活断层探测和深部构造研究等提供依据。
地震学中通常采用主动源探测或被动源成像的方法获取地下浅层速度结构，采用人工震源激发的折射波、反射波、面波等主动源探测方法具有震源位置和发震时刻已知、激发能量可控、分辨率高的优点（张明辉等，2020；刘国峰等，2021），但是由于探测成本偏高、探测深度有限、在城市布设采集困难和不够环保等原因，限制了其应用场景。与之相比，地震被动源方法是一种基于天然地震和背景噪声的无源成像方法，天然地震数据成像方面，由于地震事件时空分布不均，固定或宽频带地震台阵的台间距较大，同时受限于观测成本，难以满足对特定区域地壳浅层精细结构的研究（Lietal，2014）。背景噪声成像基于两个台站记录到的连续地震噪声计算互相关函数并叠加，近似得到台站间的经验格林函数，并从中提取面波频散曲线以反演横波速度结构（Aki，1957；Shapiroand Campillo，2004；Yaoetal.，2006）与基于天然地震事件的成像方法相比，背景噪声面波层析成像方法不依赖于地震的时空分布，可对地震活动性低的地区开展研究。
面波的频率和其探测深度之间存在紧密的联系：低频面波对深部结构比较敏感，高频面波对浅层结构比较敏感（夏江海等，2015)。近年来随着大量成本低廉、布设便捷的短周期地震仪的广泛应用，研究人员可以根据探测目标的空间特征在研究区域布设不同台间距的短周期密集台阵，通过提取地震背景噪声中的面波信号来研究特定区域的浅层地壳结构，目前，该方法已在城市、沉积盆地、断裂带、水库等浅层结构探测方面得到了初步应用（王爽等，2018；梁锋等，2019；Mordretetal.，2019；Guetal.，2019；Lietal.，2020；李玲利等，2020；曾求等，2020；田原等，2020；刘国峰等，2021；Xuetal.，2021；Shaoetal.，2022）。这些研究中利用背景噪声面波层析成像方法反演获得的横波速度结构与地质构造、重力、大地电磁、钻孔、地震活动性等相关性较好，且空间分辨率较大多数的传统方法有一定提升。但是，上述研究中所用的台间距往往较大，高频面波提取困难，因而浅部横向分辨率较低，获得的速度模型仍然难以精细刻画城市地下结构和断裂带几何特征。
因此，提取稳定可靠的高频面波频散曲线是高分辨率浅层面波勘探的关键。面波多道分析（Parketal.,1999；夏江海等，2015）是近年来常用的高频面波分析方法，可用F-K变换（Capon,1969;卢建旗，2013）、τ-p变换（Mc Mechanand Yedlin,1981;邵广周和李庆春，2010）、相移法（Parketal.，1998）、拉冬变换法（Luoetal.，2009）等方法提取频散曲线。其中相移法在计算效率、抗噪性和灵活性等方面都优于F-K法、τ-p变换方法（Dal Moroetal.，2003），具有稳定性高、能够有效提取高频面波频散曲线的优势，但是其缺点是不易提取低频频散曲线。随着浅地表勘探对探测深度的要求日益增加，急需发展一种在不降低分辨率的条件下能够有效改善低频信号质量的方法。基于背景噪声和相移法的特点，Deng等(2022)发展了一种新的方法—拓距相移法。该方法分为阵内相移和阵外相移两部分，利用阵内相移提取中高频的频散信息，用阵外相移提取中低频的频散信息，然后将两部分频散通过加权叠加获得更宽频带的频散曲线，从而保证对浅层结构具有较高分辨率的同时增加对深部结构的约束。Deng等(2022)将该方法应用于在湖南沃溪布设的8条密集测线中，提取了0.1~2s的Rayleigh波相速度频散曲线，并通过反演获得了沃溪矿区2.5km深度以浅的横波速度结构。经与已知地质剖面资料对比，表明反演的地震横波速度与断层、岩性分界面及矿脉有着很好的对应关系。
为了检验拓距相移法在城市活断层探测中的有效性，本研究组在安徽明光市横跨郯庐断裂带东界两条主干断裂布设了133个短周期地震仪，组成密集线性台阵，获得了约28天的垂直分量的连续波形数据，利用拓距相移法，我们提取了10Hz~2.0s的基阶Rayleigh波相速度频散曲线，反演得到了近地表1.3km以浅的高分辨率S波速度结构，并将其与基本重合的主动源S波反射剖面进行了分析对比。同时，结合以往地质、电法、人工地震等研究成果，详细讨论了郯庐断裂带东界两条主干断裂在明光地区的特征，利用拓距相移法及密集线性台阵采集的被动源数据，我们在近地表100m以浅获得了与主动源S波反射剖面和地质资料基本一致的反演结果，但同时反演深度大大提高，表明基于拓距相移法的线性台阵背景噪声方法可作为城市活断层探测中高精度成像的一种新的有效手段，本文的研究结果可以为明光市的地下结构和活断层探测，抗震设防，以及郯庐断裂带安徽段的演化过程等提供重要的基础数据。
郯庐断裂带是我国东部最大的一条巨型断裂带，走向总体呈北北东，在中国境内的延伸长达2400km（徐嘉炜和马国锋，1992；朱光等，2004），郯庐断裂带安徽段属于郯庐带中南段，呈北东向延伸，长约400km，宽约20~40km，该段西侧为华北板块，东侧为扬子板块，南北两端分别切割大别山造山带和苏鲁造山带（国家地震局地质研究所，1987）。自东向西，郯庐断裂带安徽段有嘉山-庐江断裂（F1）、池河-太湖断裂（F2）、朱顶-石门山断裂（F3）和五河-合肥断裂（F4）4条主干断裂（图1)（安徽省地质矿产局，1987），在研究区域内，这4条断裂走向近南北至北北东，断层面主要向东倾，局部西倾，倾角60°~80°，总体表现为两侧上隆中间陷落的“地堑”式结构（安徽省地质矿产局，1987)。
郯庐断裂带安徽段活断层主要出现在断陷盆地的边界，自南向北沿合肥盆地东界与大别山造山带东界，嘉山盆地的东、西边界展布，嘉山盆地为白垩纪伸展活动中发育的陆相地堑式盆地，整体呈南北向展布，受控于东、西边界上北北东向走向的正断层活动（Zhuetal.,2012）。野外调查表明，嘉山盆地东界上的活断层沿盆缘主断层或旁侧反向断层上发育，主体向西陡倾，而盆地西界上的活断层向东陡倾，东西界的活断层皆呈现为破碎型活断层，指示为早期盆缘正断层在新构造期的复活，在运动学上表现为逆右行平移活动（刘备等，2015)。
本研究布设的短周期线性密集台阵横跨嘉山盆地东界处郯庐断裂带的两条主干断裂：嘉山—庐江断裂（F1）和池河-太湖断裂（F2）（图1)，嘉山-庐江断裂为郯庐带东界断裂，是华北板块与苏鲁造山带交界断裂，在卫星图片上有清晰的显示，新活动性不明显，为早中更新世断裂（汤有标等，1988），其北端并没有止于嘉山而是向北延伸（刘备等，2015）。池河-太湖断裂具有明显的航磁线状异常特征，断面直立，其切割深度推测在28km以上，是隐伏于深部的走滑断裂和浅部伸展断裂的综合反映（张交东等，2010）。在女山湖以北最新活动时代为晚更新世晚期至全新世早期，女山湖以南隐伏于嘉山盆地之下，最新活动时代不确定，再往南进入合肥盆地后，活动性减弱，为早中更新世断裂（朱光等，2004；杨源源等，2017；姚大全等，2017；赵朋等，2017)。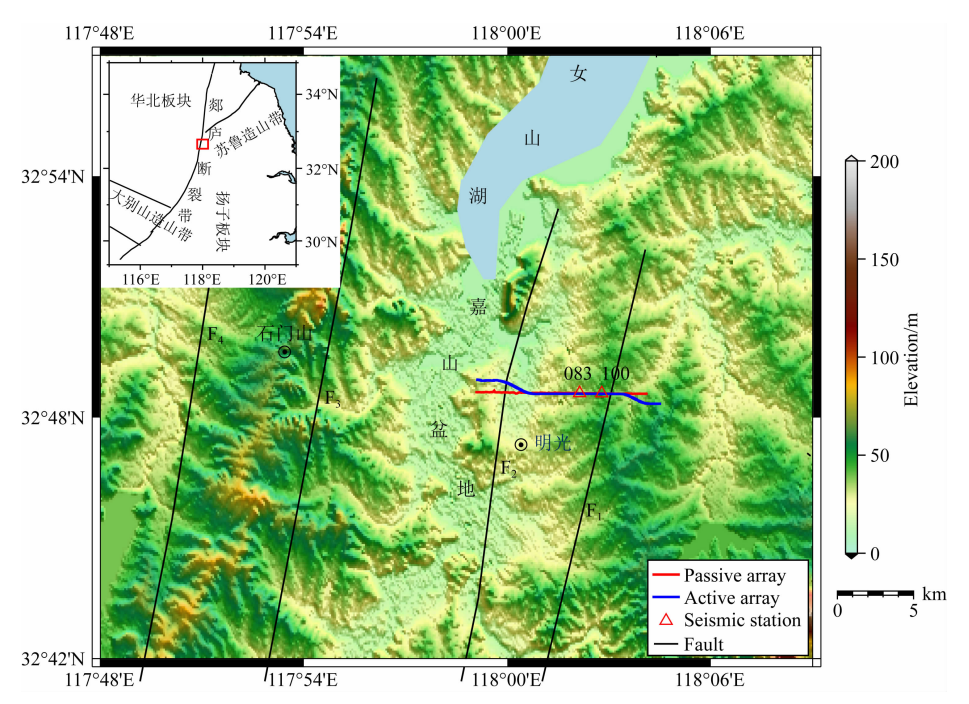
图1 研究区构造及测线位置分布图（研究区构造位置见左上角插图，大图位置见红框）
红色实线为被动源密集测线，蓝色实线为人工浅震剖面，黑色实线表示断裂：F1 嘉山-庐江断裂；F2 池河-太湖断裂；F3 朱顶-石门山断裂；F4 五河-合肥断裂
1）拓距相移法
被动源相移法是一种能够有效提取高频面波频散信号的多道面波分析方法（夏江海等，2015），但受所用台站孔径的影响不易提取低频信号．为了更为有效地提取中低频信号，本文应用最新发展的拓距相移法（Dengetal.，2022），该方法由阵内相移和阵外相移两部分组成。图2为一条密集线性台阵的示意图，假设台站等间距布设，一共有N个台站。实际应用时，拓距相移法同样适用于非均匀布设的线性台阵．当提取红色台站的频散曲线时，以该台为中心，孔径为2r范围内的台站构成一个子台阵，处于圆内部的台站（红色台站＋黑色台站）为阵内台站，处于圆外部的台站（灰色台站）为阵外台站。
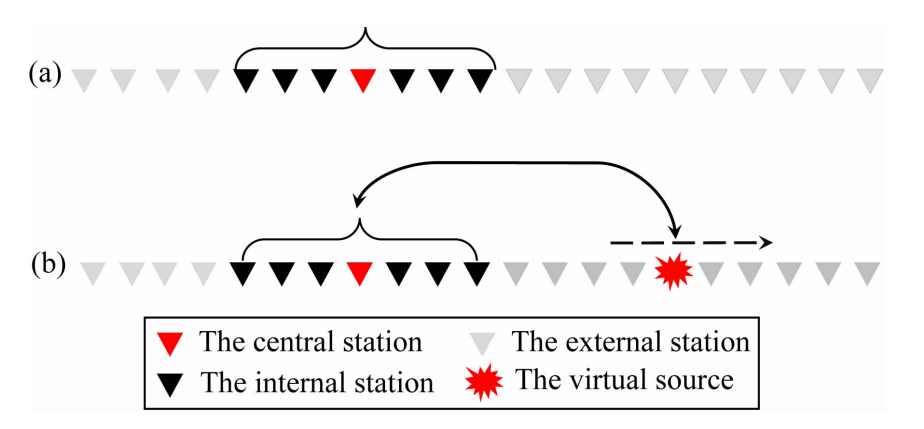
图 2 拓距相移法示意图
(a) 阵内相移 ；(b) 阵外相移
红色爆炸图标为虚拟源，倒三角为接收台站，以 一定孔径为半径划分子台阵：红色台站 黑色台站为阵内台站，灰色台站为阵外台站
阵内相移
阵内相移仅涉及子台阵内部的台站，类似于传统相移法．假设以第h个台站为中心台站（红色台站），以台间距的j倍为半孔径（r）划分子台阵．考虑最普遍的情况，即中心台站到线阵任一端的距离大于r（j＜h且h＋j＜N），则子台阵内部包含2j+1个台站（红色台站＋黑色台站），外部包含N-2j-1个台站（灰色台站），为了提高传统相移法频散成像的效果，本文将互相关函数与传统相移法结合，在相移法基础上，将所有道之间的相位差信息包含进来参与扫描叠加，首先对子台阵内所有台站两两计互相关函数，再采取与伍敦仕等(2017)提出的互相关相移法类似处理，获得该子台阵的频散能量（Dengetal.,2022）：
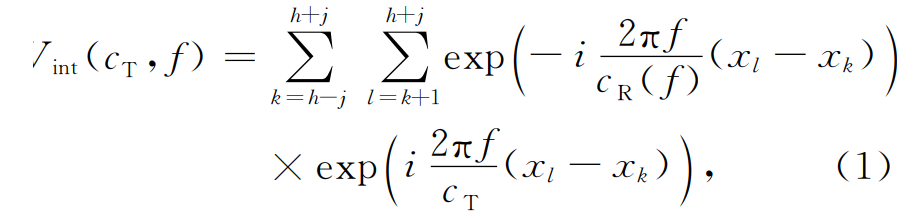
子台阵的频散能量。CR（f）表示在频率f时子台阵下方的平均相速度，Xk和Xl分别表示台站对k和l的位置。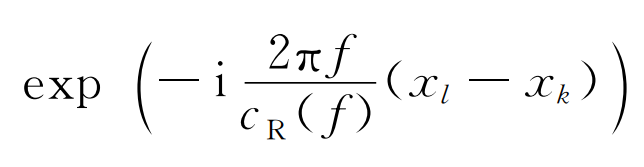
表示平面波从台站k传到台站l时的观测相移，可以直接在频率中计算，也可从互相关函数的傅里叶变换中提取。当CT=CR（f）时频散能量达到最大值，因此，我们对目标频率f进行速度扫描，用频散能量最大值对应的速度CT来估计真实的相速度CR（f），再通过扫频获得该子台阵的频散能量Vint（CT，f），作为中心台站（红色台站）的频散能量．最后通过移动中心台站获得全部台站的频散能量图。
阵外相移
阵外相移不再局限于子台阵内部，而且使用了子台阵外部的数据，以上述同样的方式划 分子台阵，对于一个子台阵，将阵外台站（灰色台站）视为虚拟源（爆炸星形），阵内台站视为接收器（红色台站＋黑色台站）．同样考虑中心台站到线阵任一端的距离大于半孔径r的最普遍情况，对子台阵外的第k个源，计算该源和子台阵内全部地震台站的频散能量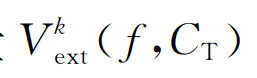
(Denget al. , 2022)
式（2）中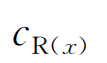
和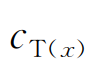
分别表示在位置的真实相速度和扫描相速度，将传播路径分为阵内、阵外两部分，得到
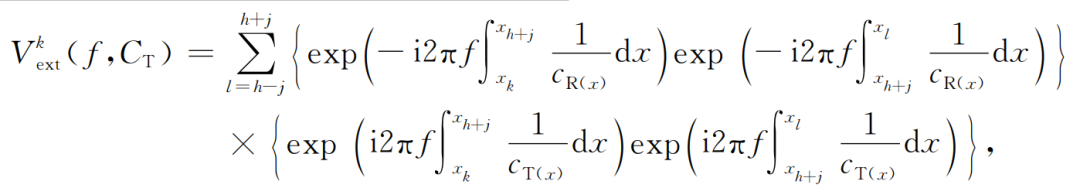
把公共的阵外路径部分提出，考虑到子台阵下方与阵内相移同样的层状介质的假设，式（3）可以简化为
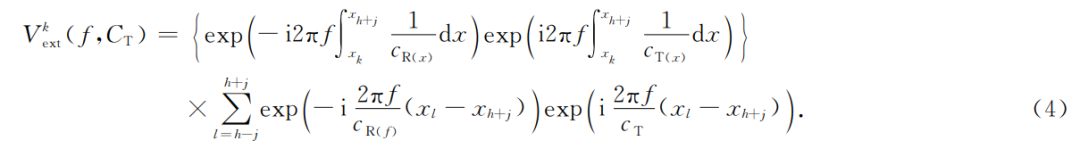
虽然不同源到同一子台阵的路径不同，但中低频信号的波长较长，衰减较慢，不易散射，在子台阵的外部区域传播路径可认为近似一致，阵外相移中对频散能量起主导作用的仍是子台阵内部区域．因此对于中低频信号，可以将对不同虚拟源得到的频散能量叠加获得的频散能量视为子台阵中心台站（红色台站）的频散能量。
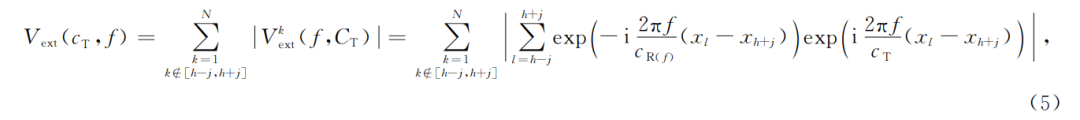
当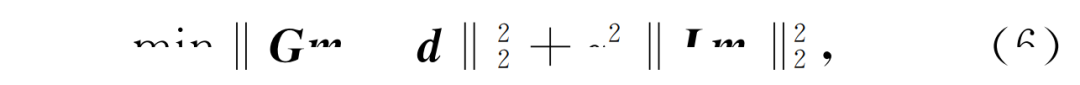
时频散能量达到最大值，与阵内相移类似，采用频率扫描、速度扫描和滑动中心台站的方式获得全部台站的频散能量图．高频信号由于衰减快、易散射、受地表起伏影响更大，其在阵外区域的传播路径较为复杂，不一定满足传播路径近似一致的假设．因此，阵外相移更适用于中低频信号的频散提取。
综上所述，阵内相移适用于提取高频信号，阵外相移适用于提取中低频信号。拓距相移法分别利用阵内相移、阵外相移提取中低频频散和中高频频散，再按照一定的权重整合成一条宽频带的频散曲线。
2）反演方法
本文通过阻尼最小二乘法，基于拓距相移法提取的宽频带频散曲线反演沿测线的横波速度结构， 反演的最小化目标函数为（Denget al. , 2022）
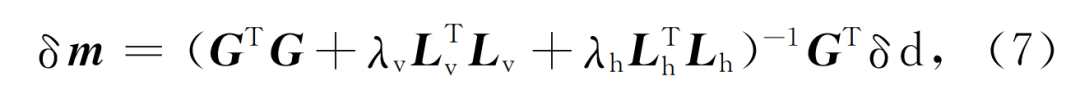
其中d为观测数据，即相速度频散曲线，m为横波速度模型，G为敏感度矩阵，L为模型的Tikhonov/Laplace正则化算子，α为阻尼系数．根据如下方程计算速度模型更新量：
式（7）中δd为观测值与现有模型理论值的偏差，G为敏感度矩阵，λv为垂直方向的阻尼因子，Lv为垂直方向有限差分近似下的拉普拉斯算子，λh为水平方向的阻尼因子，Lh为水平方向有限差分近似下的拉普拉斯算子，δm为一次迭代的模型速度修正量.式(7)括号中第一项用于反演速度结构，第二项用于约束模型垂向变化，第三项用于约束模型水平变化，提高反演结果的稳定性。
1）数据采集
本文与明光地震小区划开展的主动源浅层地震勘探（图 1中蓝线所示）同期，沿主动源测线布设了一条被动源密集测线（图 1中红线所示）。测线横跨 郯庐断裂带东界两条主干断裂：F1 嘉山-庐江断裂和 F2 池河-太湖断裂，主动源测线沿城市道路布设 所以略有弯折，跨度约8.1km , 道间距1m 、炮间距5m , 采用横波反射勘探（根据明光市城区地震小 区划隐伏断裂浅层地震探测项目报告 ”）。被动源数据采集采用节点式三分量检波器，型号为 SmartSolo 的 IGU-16，其自然频率为 5Hz，总计部署 133个台站（编号3-135 , 由西到东编 号逐渐增大），台间距约为60m ，测线跨度约 8km。观测时间自2020年11月13日至 2020年12月28日，单台最长观测时间 31天，最短 22天 。
2）数据处理
数据处理包括对133个台站记录的垂直分量连续背景噪声数据进行预处理、计算互相关函数、提取基阶Rayleigh波相速度频散曲线和反演速度结构等流程。
数据预处理和计算机相关
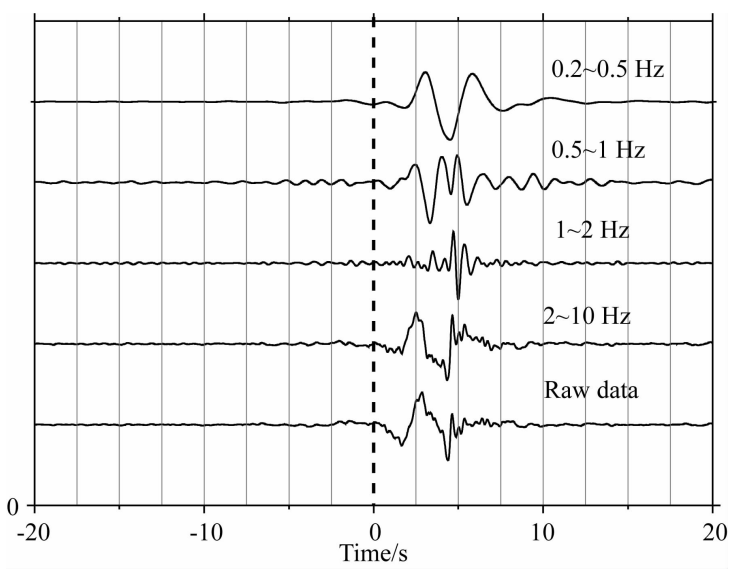
数据预处理遵循 Bensen等（2007）的处理流程，首先检查单台连续波形的数据质量并剔除坏道，将垂直分量波形切成单小时数据片段，对数据片段分 别进行去均值、去趋势，同时考虑到整条测线采用同一种地震仪器，因此无需进行去仪器响应。随后，将原始的500 Hz采样数据重采样至100Hz ，以提高计算速度，并进行10 Hz-10s带通滤波，接着进行时域归一化 、频域谱白化。最后，将所有台站两两组合，对于每一个台站对，利用对应的单小时片段计算互相关，并对所有小时的互相关函数进行叠加，以提高信噪比．通过计算，共从 133个台站的地震背景噪 声数据中计算了8778个Rayleigh波互相关函数，图3为台站 83和台站100（图 1中两个红色三角形 所示）在不同频带的互相关波形信号，从中可以看出 Rayleigh波在不同周期显示出明显的速度差异，即Rayleigh波频散现象．图4展示了三个不同滤波频段范围内台站83和其他部分台站（间距在3.2km 以内）之间的互相关波形，可以看出计算得到的Rayleigh面波信噪比较高，高频 Rayleigh波信号均可以得到很好地恢复，此外图3 、图4显示正负半支 的信号不对称，表明噪声源分布并不均匀，具有一定的方向性。
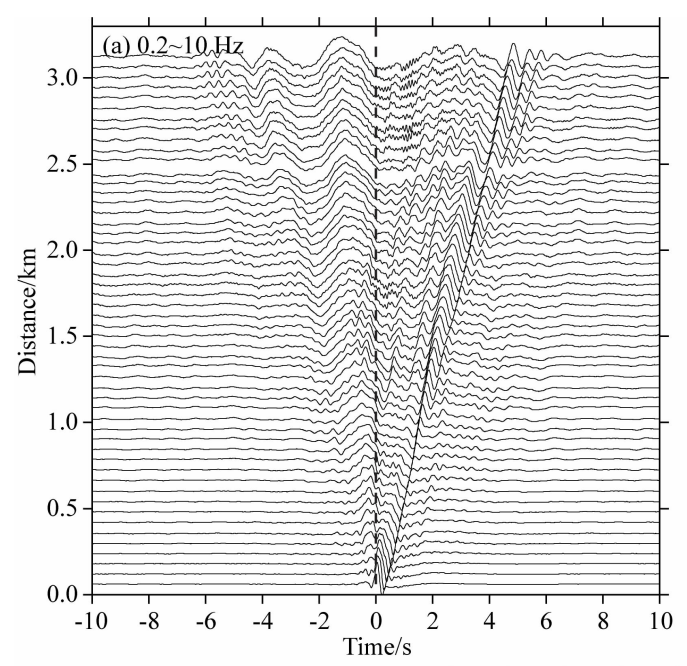
图3 台站83与台站100在不同频带的互相关波形
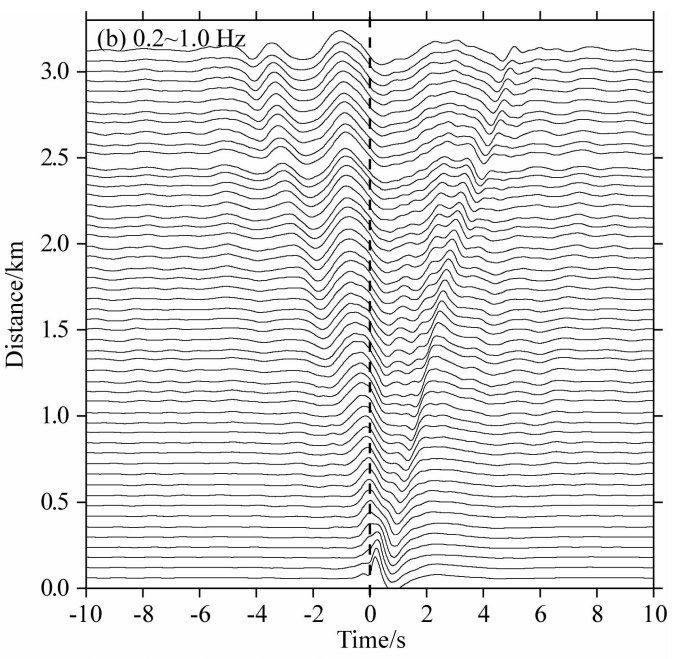
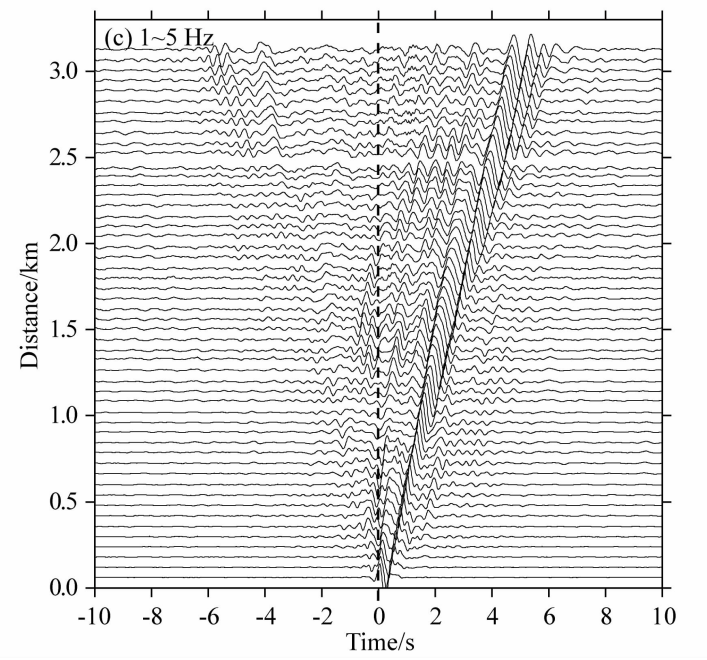
图4 台站83与其他部分台站之间的互相关波形
滤波频带分别为(a)0.2~10Hz、(b)0.2~1Hz、(c)1~5Hz, 虚线为零时间线
频散曲线提取
通过希尔伯特变换可从互相关函数中提取出经验格林函数（Yaoetal.，2006）。本文采用拓距相移法从互相关函数中计算频散能量图并提取Rayleigh波相速度频散曲线。通常情况下采用正负两支叠加平均的方法来压制噪声源不均匀带来的影响（Yangetal.，2007）。但考虑到线性台阵的互相关函数中正、负支分别代表来自两个不同端的噪声源，为避免正负两支叠加平均过程中有效信号被噪声湮灭，本文分别采取正支、负支、正负两支叠加平均3种方式计算频散能量，为频散曲线提取提供更多选择。
在计算频散能量时，对于阵内相移，子台阵孔径设为250m,扫描频段为1~10Hz;对于阵外相移，子台阵孔径设为430m,扫描频段为0.1~5Hz.图5为分别利用阵内相移和阵外相移计算的台站83的频散能量图，其中右下区域随着频率线性增长的黄色直线为空间假频。从图5中可以看出，在中高频(4~6.7Hz),采用阵内相移计算得到的频散能量更集中。连续性更高；在中低频（2Hz~1.5s）。采用阵外相移计算得到的频散能量更集中．通过比较阵内、阵外相移上、中、下三幅子图可以看出，正支的频散能量优于负支的，这与互相关函数（图3、图4）表现出的特征相吻合，需要注意的是，阵外相移提取的中低频频散信息对应于中长波长面波，本身的分辨率较低，因此适当增加子台阵孔径并不会额外牺牲横向分辨率，而简单地扩大阵内相移台阵孔径并不能得到和阵外相移在低频段同样的效果，这主要是由于源-检距的区别以及阵外相移可以进行多个虚源的叠加，极大地增强频散能量图的信噪比（Dengetal.，2022）。
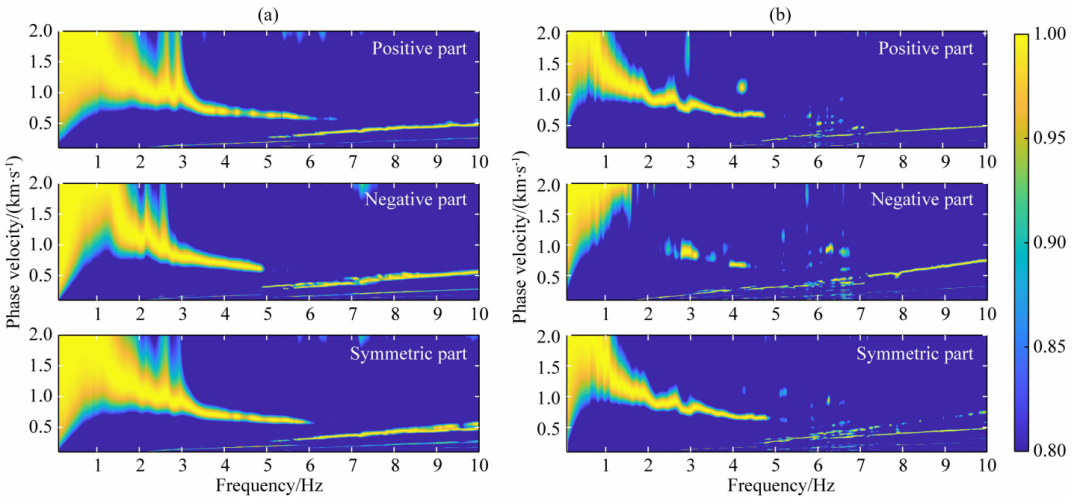
图5 利用拓距相移法得到以台站 83为中心的子台阵频散能量图
(a)阵内相移结果 ；(b)阵外相移结果．上 、中 、下三幅子图分别表示利用互相关函数的正支 、负支 、对称叠加支计算的频散能量，色标表示归 一 化的频散能量
图6为提取的整个测线基阶Rayleigh波的相速度频散曲线．阵内与阵外相移提取的频散曲线在2~4Hz范围内相速度比较一致（图6a）。因此在该频带内将阵内、阵外频散曲线采用加权叠加，从4Hz到2Hz，阵内相移的权重从1线性变化到0，相应地阵外相移的权重从0线性变化到1，频率为4Hz以上的高频采用阵内相移频散曲线，2Hz以下的低频采用阵外相移频散曲线，得到整合后的10Hz~2.0s的频散曲线（图6b).从整合后的频散曲线推断，研究区域速度变化较大，例如在1.0s周期，相速度从0.45km·s-1变化到1.5km·s-1。
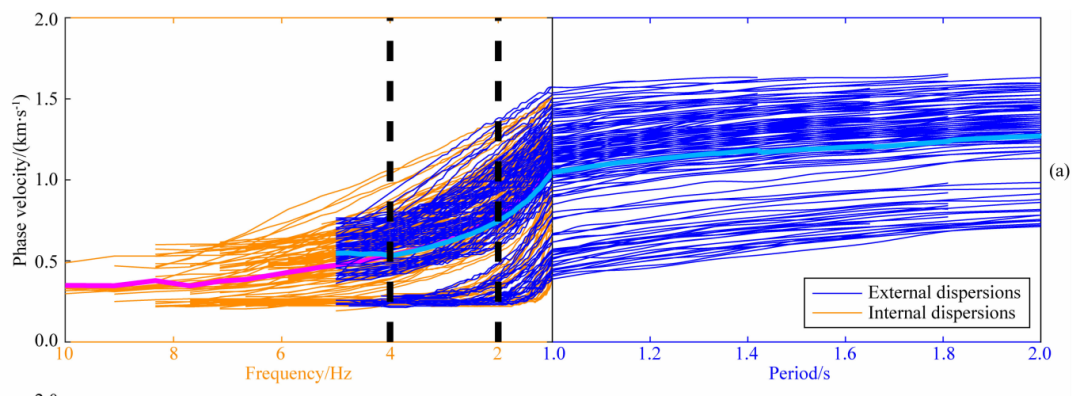
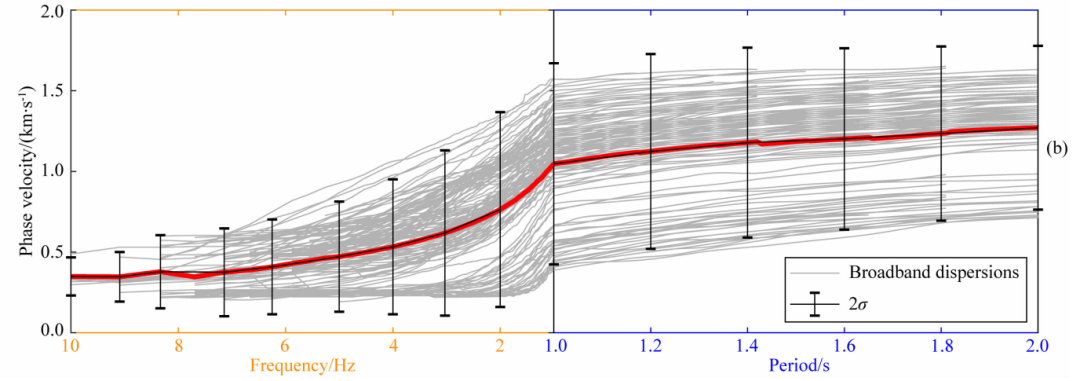
图6 (a) 分别利用阵内相移（橙线）和阵外相移（蓝线）提取的频散曲线，红线和淡蓝线分别为阵内相移和阵外相移的平均值，黑色虚线为融合频段；(b) 融合后的频散曲线（灰线）、误差棒为 2倍标准差 、红线为其平均值
反演速度结构
由于Rayleigh波相速度对1/3波长深度范围的横波速度结构最为敏感（徐果明等，2007）。我们根据相速度频散曲线，计算每个周期对应深度的平均S波速度，得到的一维平均S波速度模型作为初始模型（Xiaetal.，1999）（图7a），并计算了0.1~2.0s周期范围内不同频率的基阶Rayleigh波相速度随深度的敏感核（图7b）。可以看出随着周期的增长，相速度对应的敏感深度增加，在1.3km以浅敏感度高，表明本文提取的相速度频散曲线大致可以反演沿测线近地表1.3km以浅的S波速度。
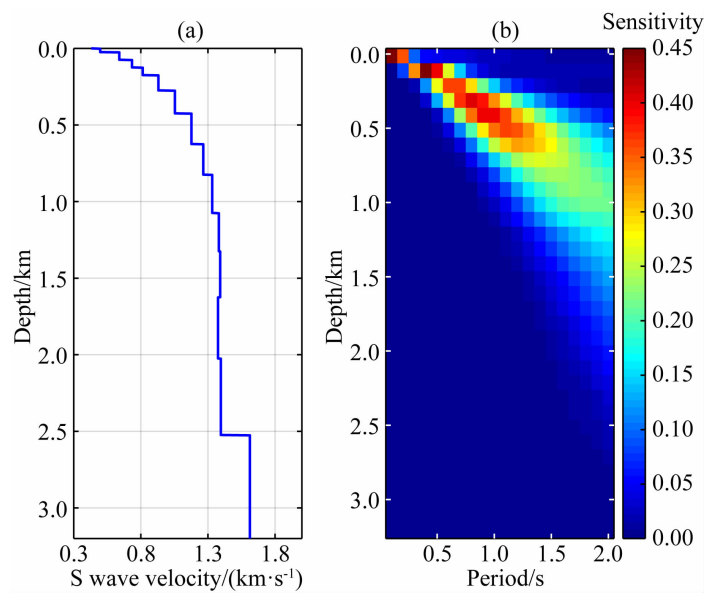
图7 (a) 一 维平均 S波速度初始参考模型；(b) 不同周期的相速度的敏感核
在速度反演中，我们设置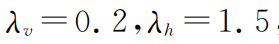
根据式（7）进行5次迭代得到了沿测线的横波速度结构（图8），图8a为地表海拔高程，变化范围为14~46m，图8b为对高程补偿后的横波速度结构，呈现明显的横向非均匀性和纵向成层性。测线西段（1~4km）在1.2km深度以浅存在一个大型低速体，而测线中段（4~6km）在0.2km深度以浅则为相对高速体，测线东段（6km以东）在0.2km深度以浅存在一个小型低速体，横向上呈现出低速-高速-低速相间分布的特点，较好地对应了地表高程显示的凹陷-隆起-凹陷相间分布的构造形态，而速度突变处可能反映了断裂的存在。
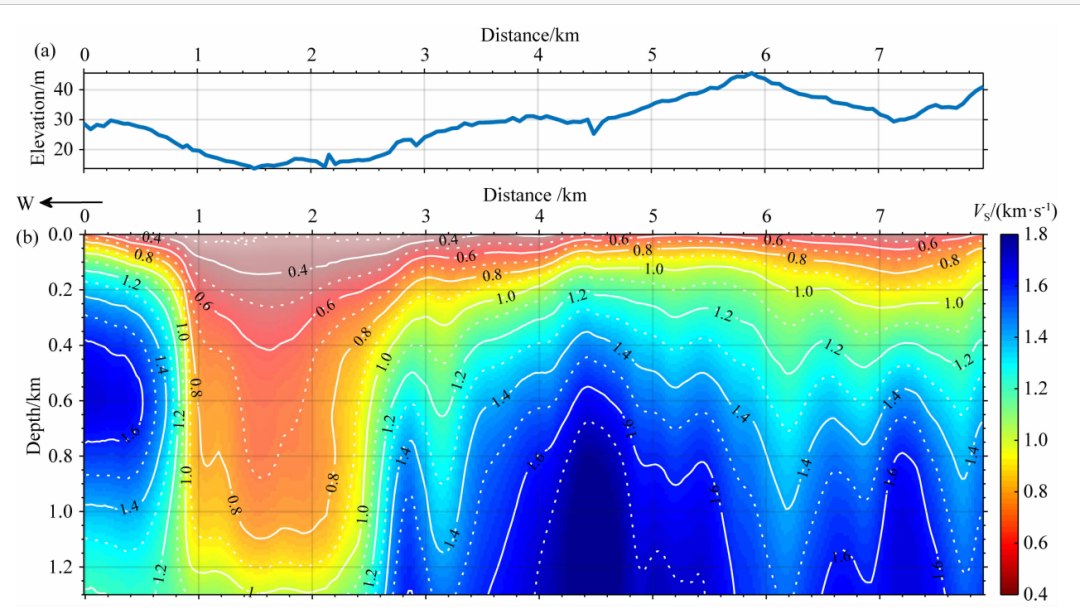
图8 (a) 沿测线的地表海拔高程；(b) 采用拓距相移法提取的宽频频散曲线反演获得的沿测线地下 S波速度结构
由于主动源测线沿城市道路布设，而被动源测线采取线性布设，两者并不完全重合．为了便于对比，我们将主动源测点垂直投影到被动源测线上，截取相同距离的测线进行比较。同时，利用Dix公式（Yilmaz,1987）将S波均方根速度转换到层速度，图9为投影后的主动源S波偏移时间剖面和结果解释（图9a)、主动源S波均方根速度（图9b)、主动源S波层速度（图9c),左边纵坐标为双程走时，右边纵坐标为按照225m·s-1的平均速度对双程走时进行时深转换后的深度，最大转换深度约为100m。
1）主动源结果及其解释
主动源S波偏移的时间剖面（图9a）的信噪比较高，揭示测线的地层反射波较为丰富。测线西段距离1~3km存在一个中生代凹陷，断层F2为凹陷的东边界。测线距离3.3km两侧为凹陷交接，推测为一逆断点DF2，距离3.9km东侧总体为一凹陷。距离5.7km附近形成一正断点F1.在距离7.3km和7.5km附近为凹陷和隆起交接地段，形成断点DF1和DF3。结合S波偏移时间剖面以及附近钻孔的结果，推测F1断裂浅部是一条倾向北西的正断层，该断裂错断古近系地层，向上未穿透第四系地层；推测出F2断裂浅部是一条倾向北西的正断层，上陡下缓，该断裂向上穿透第四系地层，可能为第四纪断裂（据“明光市城区地震小区化隐伏断裂浅层地震探测项目报告”）。
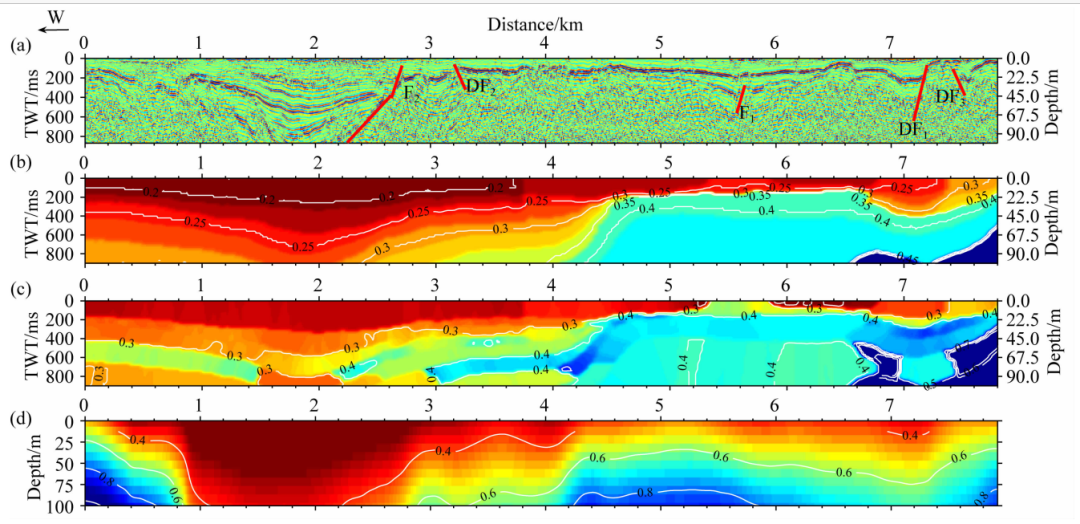
图9 (a) 主动源 S波偏移时间剖面和结果解释，(b) 主动源 S波均方根速度，(c) 主动源 S波层速度，和(d) 被动源浅层 100m的 S波速度结构对比图等值线上的数字为 S波速度，单位为km·s-1 (c) 中的高低速夹层可能是 Dix公式转换均方根速度过程中的假象
2）被动源、主动源结果对比
图9d为采用拓距相移法反演的100 m以浅的S波速度结构，从图9a 、9b 、9c的对比可 以看出：被动源结果显示测线西段距离1 ~ 3km在1.2km深度以浅存在 一个大型低速体，该低速体与主动源和高程数据刻画的中生代凹陷在近地表100m以浅高度一致，但主动源探测深度未达到该凹陷的底界， 而被动源结果清晰地显示该凹陷的底界；被动源低速体的东边界与主动源刻画F2的断点位置一致，倾角一致，且被动源的反演深度更深，能够清晰地看出断裂在1.3km深度以浅的延展情况．测线距离3.3km 两侧为两个低速体交接，主动源在此刻画 一 个逆断点DF2 , 测线距离3.3~4.4km为小型低速体，4.4~5.7km为相对高速体，5.7km东侧总体为相对低速 体，距离5.7km处为高低速的交界，总体与主动源刻的正断点 F1位置基本一致，但是速度变化不显著，在距离7.3km附近为低速与高速的过渡区域，主动源刻画了两个断点 DF1和DF3。
总之，被动源反演的S波速度结构与主动源S波偏移时间剖面的形态在近地表100m以浅高度 一致，主动源刻画的层序断点均处于被动源反演的S波高低速交界处，且主动源最大深度约为100m , 被动源的反演有效深度约为1.3km , 从被动源反演的 S波速度结构能够清晰地看出凹陷和隆起的构造 形态以及断层在更深处延展情况。
3）分析讨论
郯庐断裂带自中生代以来经历了强烈的左行平移、伸展和挤压等复杂多变的演化过程，这些演化过程必然会在深部和浅部结构上有所反映，并留下其演化的印迹（朱光等，2002，2008，刘保金等，2015），本文通过被动源和主动源刻画的F1、F2断裂分别与前人研究的嘉山-庐江断裂和池河-太湖断裂的位置相对应，这两条断裂处于嘉山盆地的东侧，Zhu等（2012）、刘备等（2015）野外调查表明嘉山盆地为白垩纪伸展活动中发育的陆相地堑式盆地，其东界断裂为北北东走向、主体向西陡倾的正断层；张交东等（2010）、秦晶晶等（2018）依据电法、人工地震等分析认为池河-太湖断裂在浅层为西倾的正断层，这些研究均与本文刻画的池河-太湖断裂特征一致，值得注意的是这些研究虽然涵盖了嘉山-庐江断裂，但该断裂均没有得到明确的揭示，这与本文在嘉山-庐江断裂被动源速度变化较小、主动源时间偏移剖面表层不显著的结果一致，表明嘉山-庐江断裂在明光段的展布存在不确定性。
姚大全和刘加灿（2004）通过现场调查取样、钻探分析等研究认为池河—太湖断裂池河段主要发育于晚白垩纪地层中，晚更新世以来断裂仍有活动，活动方式以逆冲蠕滑为主；嘉山-庐江断裂池河段总体走向约20°，为东倾的压性断裂，电镜扫描测试结果反映断裂在早更新世有过活动，这与本文刻画的浅部断层几何特征结论相悖．由于郯庐断裂带历经多次构造运动的强烈改造，演化时间长、空间跨度大，形成了现今复杂的构造格局，同时受限于当时的研究方法和地质理论等，在缺乏地球深部资料约束的情况下，一些观点可能存在分歧。
本文通过密集线性台阵的被动源背景噪声成像和人工浅层地震勘探，获得了郯庐断裂带东界两条主干断裂在地壳浅部的高分辨率S波速度结构及精细几何特征．结合以往地质、电法、人工地震等研究成果，综合分析认为池河-太湖断裂是隐伏于深部的走滑断裂，浅部具有伸展特征，具体表现为上陡下缓、倾向北西的正断层，向上穿透第四系地层，可能为活动断裂；嘉山—庐江断裂浅部速度结构特征不甚清晰，可能是一条倾向北西的正断层，断裂错断古近系地层，向上未穿透第四系地层。未来可进一步采用Rayleigh波和Love波、基阶和高阶模式相结合的联合反演等方法来提高反演的准确性，必要时可借助钻孔等其他探测手段开展更精细的研究工作。
基于短周期密集台阵的背景噪声面波层析成像方法具有不需要震源激发、不依赖于天然地震时空分布、可以人为调节台间距来控制分辨率、观测方便、探测成本低等优势，该方法使得低成本、大规模、高分辨率的浅层结构探测成为可能，而提取稳定可靠的高频面波，同时拓展低频面波信号是浅层结构勘探的关键和需求。为了探讨密集线性台阵地震背景噪声成像应用于城市活断层调查的有效性，我们在安徽省明光地震小区划项目开展的人工浅层地震勘探测线同期在相同位置布设一条被动源测线，该被动源测线由133个短周期地震仪组成，台间距约60m,横跨郯庐断裂带东界嘉山—庐江断裂（F1）和池河-太湖断裂（F2）两条主干断裂．通过采集的约28天的三分量连续噪声波形数据，采用最近新提出的拓距相移法提取基阶Rayleigh波宽频相速度频散曲线，基于此反演了沿测线下方的S波速度结构，并与主动源S波反射剖面结果和地质资料等进行对比，获得如下认识：
（1）通过拓距相移法的阵内相移和阵外相移分别提取了中高频和中低频的频散曲线，通过加权叠加，得到了10Hz~2.0s的基阶Rayleigh波频散曲线；反演时在单点反演基础上增加模型横向及纵向约束，获得了近地表1.3km以浅的高分辨率的S波速度结构.浅层S波速度横向上呈现出低速-高速-低速相间分布的特点，与地表高程凹陷-隆起-凹陷相间分布的构造形态对应较好。
（2）将拓距相移法反演结果与人工浅层地震勘探结果进行对比，结果表明，被动源反演的S波速度结构与主动源S波偏移时间剖面的形态在近地表100m以浅高度一致，主动源刻画的层序断点均处于被动源反演的S波高低速交界处。同时，利用被动源反演的速度结构更深，能够清晰地看出凹陷和隆起的构造形态以及断层在更深处延展情况。
（3）本文通过密集线性台阵的被动源背景噪声成像和人工浅层地震勘探，获得了郯庐断裂带东界两条主干断裂在地壳浅部的高分辨率S波速度结构和精细几何特征，结合以往地质、电法、人工地震等研究成果。综合分析认为池河-太湖断裂是隐伏于深部的走滑断裂和浅部伸展断裂的综合反映，其在浅部为上陡下缓、倾向北西的正断层，该断裂向上穿透第四系地层，可能为第四纪断裂。嘉山-庐江断裂浅部可能是一条倾向北西的正断层，该断裂错断古近系地层，向上未穿透第四系地层，但是被动源速度变化较小、主动源时间偏移剖面表层不显著，对嘉山-庐江断裂的认识需要进一步开展钻孔勘探等工作来验证。研究可为明光市强地面震动模拟、地震危险性评价、城市活断层调查和郯庐断裂带深、浅部构造特征分析等提供参考依据。
（4）拓距相移法将传统相移法与背景噪声互相关相结合，很大程度上改善了传统相移法对低频段信号提取困难的问题，拓宽了频散曲线的提取频带，在不降低浅层分辨率的前提下能够有效增加对深部结构的约束。采用拓距相移法的被动源反演结果与主动源、地质资料等均有较好的对应性，进一步表明基于该方法的线性密集台阵监测可用于浅地表及活断层成像，为城市活断层调查和城市地下空间探测提供了一种新的思路和技术手段。
（5）本文研究采集了三分量连续波形数据，部分台站的高阶面波发育，但反演时仅采用了基阶Rayleigh波频散数据。由于Love波相对于Rayleigh波往往具有更高的信噪比，频散能量更清晰，高阶模式比基阶模式对S波速度变化更加敏感、探测深度更深，因此下一步我们将采用Rayleigh波和Love波、基阶和高阶模式相结合的联合反演，进一步提高S波速度结构反演的准确性。
